Tags machine learning Date

Perceptron Implementing AND, Part 1

Learning Machine Learning Journal \#2

In Perceptron in Neural Networks, we got my feet wet learning about perceptrons. Inspired by Michael Nielsen’s Neural Networks and Deep Learning book, today, the goal is to expand on that knowledge by using the perceptron formula to mimic the behavior of a logical AND.

In this post, we’ll reason about the settings of our network that, in Perceptrons Implementing AND, Part 2, we’ll have the computer do itself.

As a programmer, I am familiar with logic operators like AND, OR, XOR. Well, as I’m learning about artificial neurons, it turns out that the math behind perceptrons, see more here, can be used to recreate the functionality of these binary operators!

As a refresher, let’s look at the logic table for AND:

 A   B  | AND
--- --- |-----
 0   0  |  0
 0   1  |  0
 1   0  |  0
 1   1  |  1

Let’s break it down.

To produce a logical AND, we want our function to output 1, only when both inputs, A, and B, are also 1. For every other case, our AND should output 0.

Let’s take a look at this using our perceptron model from last time, with a few updates:

The equation we ended up with looks like this:

[https://en.wikipedia.org/wiki/Perceptron](https://en.wikipedia.org/wiki/Perceptron)

And when we insert our inputs and outputs into our model, it looks like this:

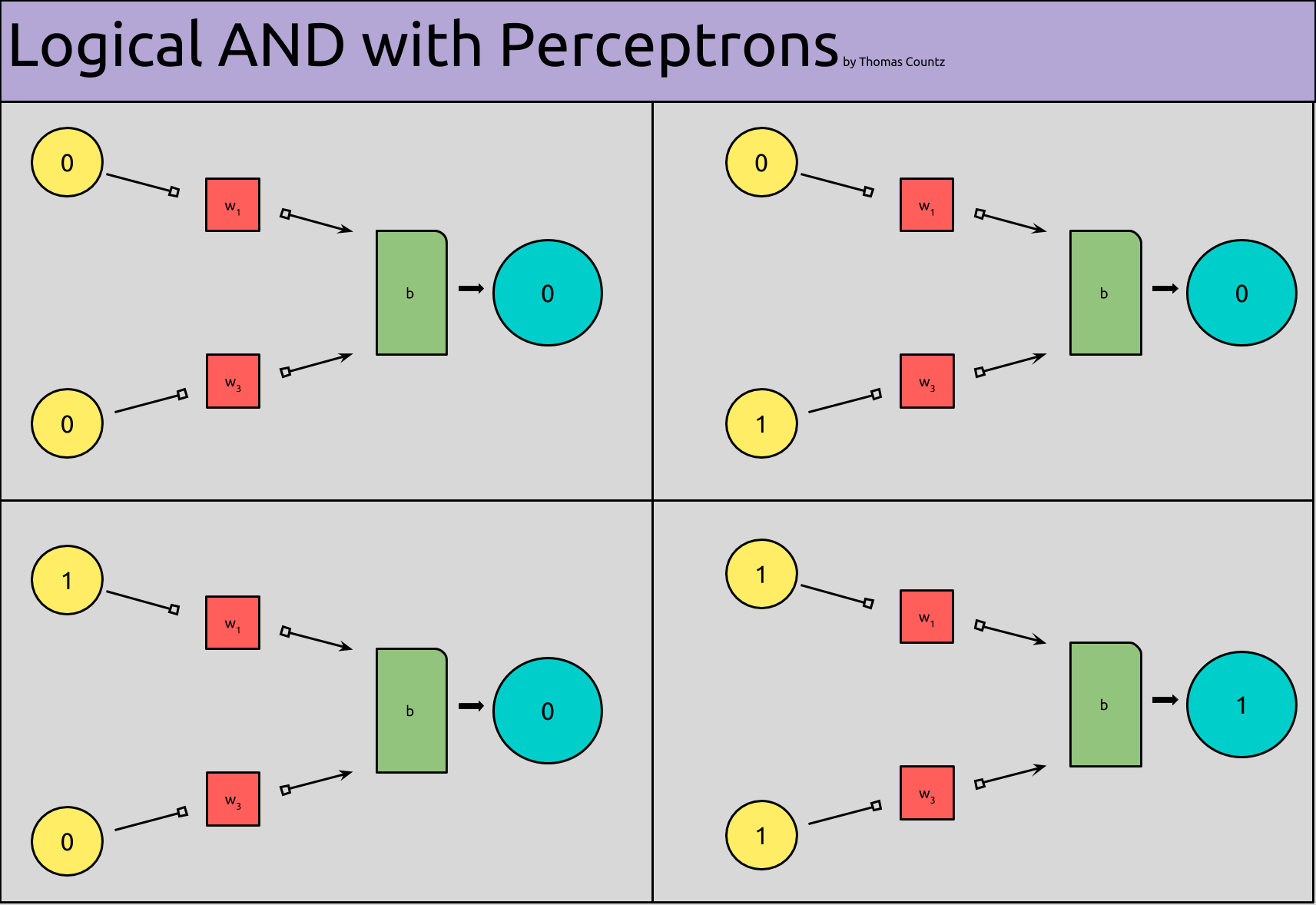
Logical AND with Perceptrons

Side note: This model of a perceptron is slightly different than the last one. Here, I’ve tried to model the weights and bias more clearly.

All we’ve done so far, is plug our logic table into our perceptron model. All of our perceptrons are returning 0, except for when both of our inputs are “activated,” i.e. when they are 1.

What is missing from our model, is the actual implementation detail; the weights and biases that would actually give us our desired output. Moreover, we have four different models to represent each state of our perceptron, when what we really want, is one!

So the question becomes how do we represent the behavior of a logical AND, i.e., what weights and biases should we input into our model to produce the desired output?

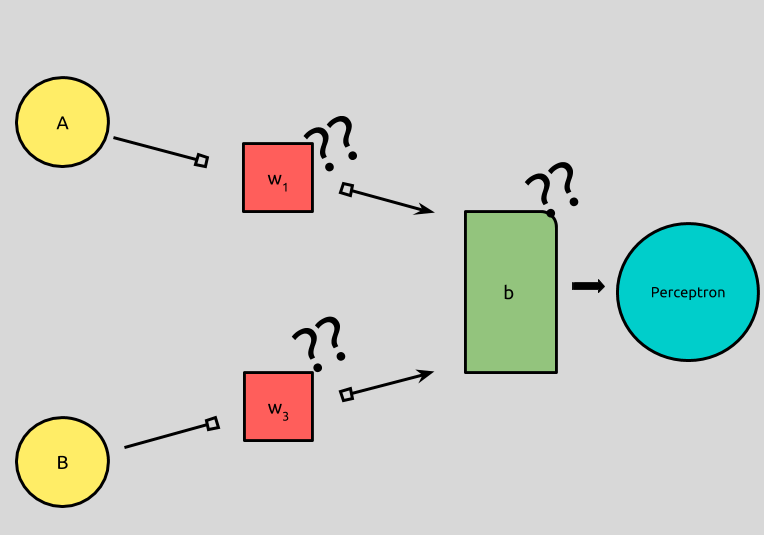
What should our weights and bias be?

The first thing to note is that our weights should be the same for both inputs, A and B.

If we look back at our logic chart, we can begin to notice that the position of our input values does not affect our output.

 A   B  | AND
--- --- |-----
 0   0  |  0
 0   1  |  0
 1   0  |  0
 1   1  |  1

For any statement above, if you swap A and B, the AND logic still stands true.

The second thing to note is that our summation + bias, w · x + b, should be negative, except when both A and B are equal to 1.

[https://en.wikipedia.org/wiki/Perceptron](https://en.wikipedia.org/wiki/Perceptron)

If we take a look back at our perceptron formula, we can generalize that our neuron will return 1, whenever our input is positive, x > 0, and return 0, otherwise, i.e., when the input is negative or 0.

Now, let’s work our way backwards.

If our inputs are A = 1 and B = 1, we need a positive result from our summation, **w · x**; for any other inputs, we need a 0 or negative result:

1w + 1w + b  > 0
0w + 1w + b <= 0
1w + 0w + b <= 0
0w + 0w + b <= 0`

We know that:

So we can simplify the above to:

2w + b > 0
w + b <= 0
b <= 0`

Now we know that:

We also know that:

That’s it!

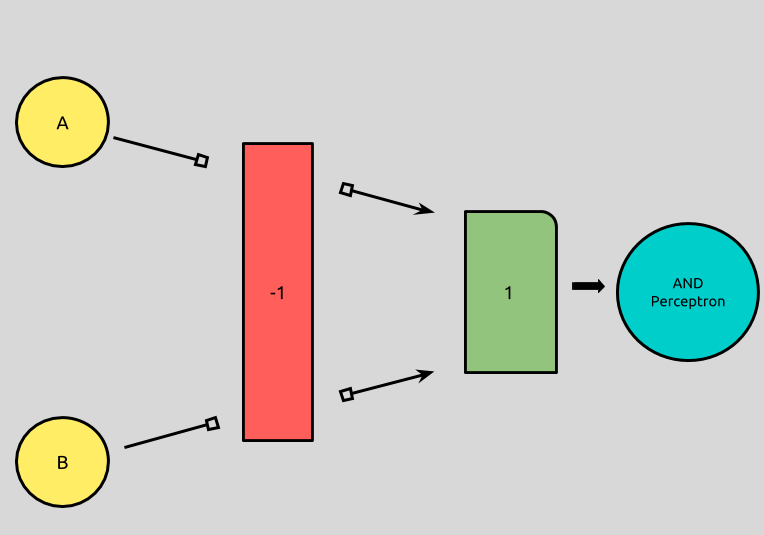
We now know that we can set b to any negative number and both w’s to its opposite, and we can reproduce the behavior of AND by using a perceptron!

For simplicity, let’s setb = 1, w1 = -1, and w2 = -1

Resources

· machine learning